حل درس حل نظام من معادلتين خطيتين بيانياً رياضيات ثالث متوسط الفصل الدراسي الثاني

حل درس حل نظام من معادلتين خطيتين بيانياً رياضيات ثالث متوسط الفصل الدراسي الثاني

تحقق من فهمك 

ص = 2س + 3

ص = -2س +3 

الجواب : 

بما أن المستقيمين اللذين يمثلان المعادلتين يتقاطعان في نقطة واحدة فهناك حل واحد للنظام و يكون النظام متسقا و مستقلا 

ص = س -5

ص = -2س -5 

الجواب : 

بما أن المستقيمين اللذين يمثلان المعادلتين يتقاطعان في نقطة واحدة فهناك حل واحد للنظام و يكون النظام متسقا و مستقلا 

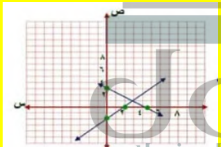
السؤال : مثل كلا من أنظمة المعادلات الآتية بيانياً، وأوجد عدد حلوله، وإن كان واحداً فاكتبه:

س -ص = 2

3ص +2س = 9

الجواب : 

س -ص = 2

عند س = 0   ص = -2   النقطة ( 0،-2 ) 

ص = 0   س = 2         النقطة ( 0،2 )

3ص +2س = 9

 عند  س = 0   ص = 3   النقطة ( 3،0 ) 

ص = 0   س = 4.5    النقطة ( 0، 4.5 ) 

 بما أن المستقيمين اللذين يمثلان المعادلتين يتقاطعان في نقطة واحدة فهناك حل واحد للنظام و يكون النظام متسقا و مستقلا 

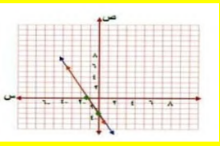
ص = -2س - 3

6س + 3ص = -9 

الجواب :     

ص = -2س - 3

6س + 3ص = -9

2س +ص = -3

ص = -2س - 3

عند س = 0   ص = -3 النقطة ( 0 ، -3 ) 

ص = 0     س = - 1.5 النقطة ( -1.5 ، 0 ) 

بما ان المستقيمين منطبقين إذا لهما  عدد لا نهائي من الحلول 

السؤال : ساعات: يرغب كل من محمود ورائد في شراء ساعة يدوية، فإذا كان مع محمود 14 ريالاً، ويوفر 10 ريالات في الأسبوع، ومع رائد 26 ريالاً ويوفر 7 ريالات في الأسبوع، فبعد كم أسبوع يصبح معهما المبلغ نفسه؟
 

الجواب : 

معادلة ما يوفره محمود ص = 10س + 14

معادلة ما يوفره رائد : ص = 7 س +26 

مثل المعادلتين بيانيا 

ص = 10 س  + 14 

عند س = 0 ص = 14 النقطة ( 0 ، 14 ) 

ص = 0   س = -1.4  النقطة ( 0، 1.4- ) 

ص = 7س +26

 عند س = 0 ص = 26 النقطة ( 0، 26 ) 

ص = 0 س = 3.7-   النقطة ( 0، -3.7 ) 

ص = 10 س +14 ضرب المعادلة في 7 

ص = 7س + 26 ضرب المعادلة في 10

7ص  = 70 س +  98   ( 1 ) 

10ص = 70 س + 260   ( 2 ) 

بطرح المعادلتين 1 و 2 و ينتج ان 

-3 ص = -162 

 ص = -162 ÷ - 3

ص = 54

بالتعويض في أي من المعادلتين عن ص = 54

54 = 10 س +14

10س = 54 -14

10 س = 40 

 س = 4 

 إذن نقطة التقاطع هي ( 4 ، 54 ) و بما ان نقطة التقاطع عند النقطة ( 4 ، 54 ) فعدد الاسابيع = 4 اسابيع

تأكد

السؤال : استعمل التمثيل البياني المجاور لتحدد ما إذا كان كل من أنظمة المعادلات الآتية متسقاً أم غير متسق، ومستقلاً أم غير مستقل

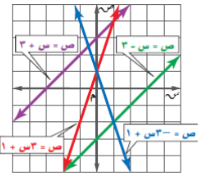
ص = -3 س + 1

 ص = 3س + 1

الجواب : 

بما أن المستقيمين اللذين يمثلان المعادلتين يتقاطعان في نقطة واحدة فهناك حل واحد للنظام و يكون النظام متسقا و مستقلا 

ص = 3س + 1

ص = س -3 

الجواب : 

بما أن المستقيمين اللذين يمثلان المعادلتين يتقاطعان في نقطة واحدة فهناك حل واحد للنظام و يكون النظام متسقا و مستقلا 

ص = س - 3

ص = س + 3

الجواب : 

بما أن المستقيمين اللذين يمثلان المعادلتين يتقاطعان في نقطة واحدة فهناك حل واحد للنظام و يكون النظام متسقا و مستقلا 

ص = س+ 3 

س -ص = -3 

الجواب : 

بما أن المستقيمين اللذين يمثلان المعادلتين يتقاطعان في نقطة واحدة فهناك حل واحد للنظام و يكون النظام متسقا و مستقلا 

السؤال : مثل كلا من أنظمة المعادلات الآتية بيانياً، وأوجد عدد حلوله، وإن كان واحداً فاكتبه:

ص = س + 4

 ص = -س -4 

الجواب :

ص = س +4 

عند س = 0   ص = 4  النقطة ( 0 ، 4 )

ص = 0   س = -4  النقطة - ( -4 ، 0 ) 

ص = -س -4

عند س = -س -4 

عند س = 0  ص = -4 النقطة ( 0 ، -4 ) 

ص = 0   س = 1.4 -   النقطة ( 0، 1.4- ) 

بما أن المستقيمين اللذين يمثلان المعادلتين يتقاطعان في نقطة واحدة فهناك حل واحد للنظام و يكون النظام متسقا و مستقلا 

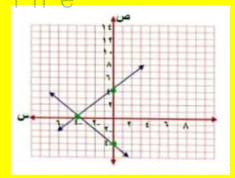
ص = س  +3 

4ص = 2س +4

الجواب : 

ص = س + 3

عند س = 0  ص = 3   النقطة ( 3،0 ) 

ص = 0   س = -3  النقطة ( 0، -3 ) 

ص = 2س + 4

 عند س = 0   ص = 4  النقطة ( 4،0 ) 

 ص = 0  س = -2  النقطة ( -2 ، 0 ) 

بما أن المستقيمين اللذين يمثلان المعادلتين يتقاطعان في نقطة واحدة  ( -1 ، 2 ) فهناك حل واحد للنظام و يكون النظام متسقا و مستقلا 

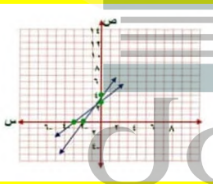
السؤال : قراءة: يقرأ كل من صالح وعبد الله قصة طويلة كما في الشكل المقابل.
 

أ- اكتب معادلة تعبر عن عدد الصفحات التي يقرؤوها كل منهما 

الجواب : 

معادلة ما يقرأ صالح = ص = 20 س +35

معادلة ما يقر أ عبد الله ص = 10س + 85

ب - مثل كل معادلة بيانيا 

الجواب :

ص = 20س +35

عند س = 0   ص =35  النقطة ( 0 ، 35 ) 

ص = 0  س = -1.75  النقطة ( 0، 1.75- ) 

ص = 10س + 85

 عند س = 0  ص = 85  النقطة ( 0 ، 85 ) 

ص = 0  س = 8.5-    النقطة ( 0،  5.8- ) 

جـ : بعد كم يوم يصبح ما قراه صالح أكثر مما قراه عبد الله ؟ تتحقق من إجابتك و فسرها ؟
الجواب : 

بعد 6 أيام يصبح ما قرأه صالح أكثر مما قرأه عبد الله 

 لان عند 5 ايام يكون عدد الصفحات متساوية لان المستقيمين الممثلين النظامين يتقاطعان عند النقطة ( 135، 5 ) و بعدها يزداد عدد صفحات صالح عن عبد الله 

للتحقق : احسب عدد الصفحات للكل منها في اليوم السادس 6×20 + 35 = 155

 عبدالله ص = 10س +85 

= 10 × 6 +85 = 145

صالح : ص = 20 س + 35

20 × 6 +35 = 155

 أي ما قرأه صالح أكثر مما قراه عبد الله في اليوم السادس 

السؤال :استعمل الرسم البياني المجاور لتحدد ما إذا كان كل نظام فيما يأتي متسقاً أم غير متسق، ومستقلاً أم غير مستقل:

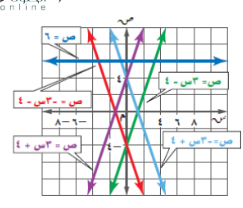
ص = -3س +4

ص = -3س -4

الجواب : بما أن المستقيمين اللذين يمثلان المعادلتين متوازيان فلا  يوجد حل للنظام و يكون النظام غير متسق

ص = -3س -4

ص = 3س -4

الجواب : 

بما أن المستقيمين اللذين يمثلان المعادلتين يتقاطعان في نقطة واحدة فهناك حل واحد للنظام و يكون النظام متسقا و مستقلا 

3س - ص = -4

ص = -3س + 4

الجواب : 

بما أن المستقيمين اللذين يمثلان المعادلتين يتقاطعان في نقطة واحدة فهناك حل واحد للنظام و يكون النظام متسقا و مستقلا 

3س -ص = 4

3س+ ص = 4

الجواب : 

بما أن المستقيمين اللذين يمثلان المعادلتين يتقاطعان في نقطة واحدة فهناك حل واحد للنظام و يكون النظام متسقا و مستقلا 

السؤال : مثل كل نظام مما يأتي بيانياً، وأوجد عدد حلوله، وإذا كان واحداً فاكتبه:

ص = 4س + 2 

ص = -2 س -3 

الجواب : 

ص = 4س + 2

عند س = 0   ص = 2  النقطة ( 2.0 )

ص = 0 س = 0.5-   النقطة ( 0، 0.5 - ) 

ص = -2س -3

 عند س = 0  ص = -3   النقطة ( 0، -3 ) 

عند س = 0  س = 1.5- النقطة ( 0، 1.5- ) 

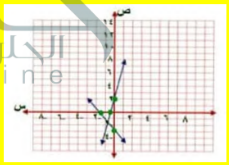
ص = س - 6

ص = س + 2

الجواب :

ص = س- 6

عند س = 0 ص = -6 النقطة ( 0، -6 ) 

ص = 0 س = 6 النقطة ( 0،6 ) 

ص = س +2 

 عند س = 0  ص = 2  النقطة ( 2،0 )

عند ص = 0 س = -2 النقطة ( 0، -2 ) 

بما أن ميل كلا المستقيمين متساوي ومقاطعهما الصادي مختلفين فالمستقيمان متوازيان لا يوجد حل للنظام و يكون النظام غير متسق 

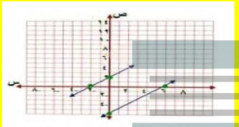
س + ص = 4

3س + 3ص = 12

الجواب :

س + ص = 4

عند س = 0 ص = 4 النقطة ( 0 ، 4 ) 

ص = 0 س = 4 النقطة ( 4، 0 ) 

3س + 3ص = 12 ÷ 3

س +ص = 4

عند س = 0  ص = 4  النقطة ( =4 النقطة ( 4،0 )

عند  ص = 0 س  ( 0،4 ) 

 بما ان المستقيمين اللذين يمثلان المعادلتين منطبقين فلهما عدد لا نهائي من الحلول و يكون النظام متسق و غير مستقل 

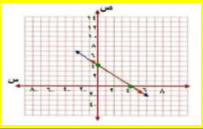
س - ص = -2

-س +ص = 2

الجواب : 

س - ص = -2

عند س = 0  ص = 2 النقطة ( 0، 2 ) 

ص = 0  ص = 2  النقطة ( -2 ،0 ) 

 -س + ص = 2

عند س = 0   ص = 2   النقطة ( 0،2 ) 

عند ص = 0 س = -2 النقطة ( -2 ، 0 ) 

 بما ان المستقيمين اللذين يمثلان المعادلتين منطبقين فلهما عدد لا نهائي من الحلول و يكون النظام متسق و غير مستقل 

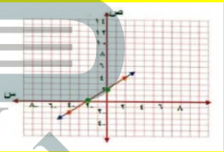
س + 2 ص  =3

س = 5 

الجواب : 

+2ص = 3

 عند س = 0  ص = 1.5 النقطة ( 0 ، 1.5 ) 

 ص = 0 س = 3 النقطة ( 3 ، 0 ) 

بما أن س = 5 ارسم مستقيم يوازي محور ص 

 بما ان المستقيمين اللذين يمثلان المعادلتين يتقاطعان في نقطة واحدة فهناك حل واحد ( 5 ، -1 ) للنظام و يكون النظام متسقا و مستقلا 

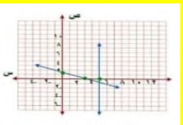
2س + ص = -4 

ص +2 س = 3

الجواب : 

2س + ص = -4 

 عند س = 0 ص = -4 النقطة ( 0 ، -4 ) 

 ص = 0 س = -2 النقطة ( -2 ، 0 ) 

---